수렴 정리

Lebeck의 적분 이론에서 매우 자주 사용되는 수렴 정리에 대해 논의할 것입니다. 이 문구를 사용하면 매우 유용한 결과를 쉽게 얻을 수 있습니다.

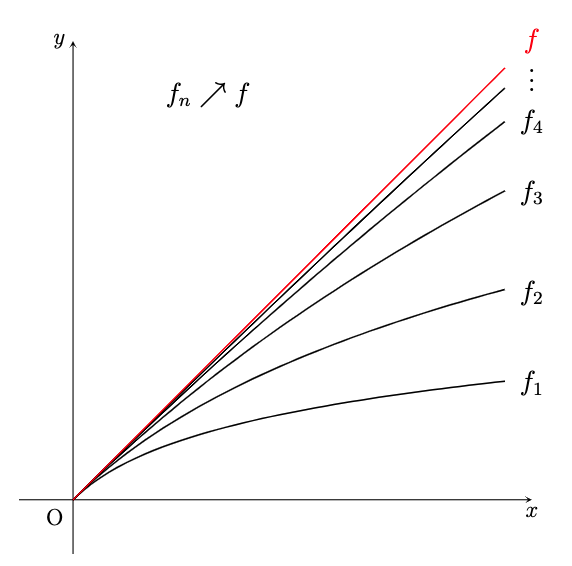
첫 번째는 단조 수렴 정리(MCT)입니다. \(f_n \geq 0\)은 이 정리에서 매우 중요합니다.

정리하다. (단조 수렴 정리) \(f_n:X\rightarrow(0,\infty)\)가 측정 가능하고 모든 \(x\in X\)\(f_n(x)\leq f_{n+1}(x ) \) . \(\lim_{n\rightarrow\infty} f_n(x) = \sup_{n} f_n(x) = f(x)\), \(\int f \,d{\mu } = \lim_ { n\rightarrow\infty} \int f_n \,d{\mu } = \sup_{n \in \mathbb{N}} \int f_n \,d{\mu }\).

입증하다.
(\(\geq\)) \(f_n(x) \leq f(x)\) 이후 모든 \(n \in \mathbb{N}\) \(\displaystyle\int f_n \ 에 대해 단조성을 사용하여 d {\mu } \leq \displaystyle\int f \,d{\mu }\). 따라서 다음 \(\sup_n \int f_n \,d{\mu } \leq \int f \,d{\mu }.\)

(\(\leq\)) 실수 \(c \in (0, 1)\) 을 잡아봅시다. 끝에 \(c \narrow 1\)을 넣습니다. 측정 가능한 단순 함수 \(s\)는 이제 \(0 \leq s \leq f\)입니다. 그러면 \(c\cdot s(x)

\(E_n = \{x \in X : f_n(x) \geq cs(x)\}\)라고 하자 \(f_n(x) – cs(x)\)는 측정 가능한 함수이므로 \(E_n \ ) 또한 측정 가능합니다. 여기서 \(f_n\)이 증가하므로 \(E_n\subseteq E_{n+1} \subseteq\cdots\)가 \(f_n \rightarrow f\)와 같다는 것을 알 수 있습니다. 즉, \(\bigcup_{n= 1} ^\ Infty E_n = X\).

\(n\geq N\)에 대해 충분히 큰 \(N\in \mathbb{N}\), \(f(x)\geq f_n(x) > cs(x)\)에 대해 유지됩니다. 그리고 \(f_n \geq f_n \chi_{E_n} \geq cs \chi_{E_n}\) 따라서 \(\tag{\(\star\)} \int f_n \,d{\mu } \geq \int f_n \chi_{E_n} \,d{\mu} \geq c\int s \chi_{E_n} \,d{\mu},\) 여기서 \(s, \chi_{E_n}\)는 간단한 함수입니다. 따라서 \(s = \sum_{k=0}^m y_k \chi_{A_k}\)로 쓰면 \(s\chi_{E_n} = \sum_{k=0}^m y_k \chi_{A_k\ cap E_n} \은 \int s \chi_{E_n} \,d{\mu } = \sum_{k=0}^m y_k \mu(A_k\cap E_n)\)를 의미합니다. \(A_k\cap E_n \nearrow A_k\) \(n\rightarrow\infty\) 이면 측정의 연속성을 사용하여 \(\mu(A_k \cap E_n) \nearrow \mu(A_k)\) \ ( \lim_{n\rightarrow\infty} \int s \chi_{E_n}\,d{\mu } = \int s \,d{\mu }\) 음, (\(\star\))는 \(\lim_{n\rightarrow\infty} \int f_n \,d{\mu} \geq c\int s \,d{\mu}\) , \(c \nearrow 1\) 및 \ ( \sup\) for \(0\leq s\leq f\) 제공 \(\lim_{n\rightarrow\infty} \int f_n \,d{ \mu } \geq \sup_{0\leq s\leq f } \int s \,d{\mu } = \int f \,d{\mu }\) 원하는 결과를 얻습니다.

참조. 부등식 \(0 \leq f_n \leq f_{n+1}\)이 정의 도메인의 하위 집합 \(E\)에만 적용되고 전체 정의 도메인에는 적용되지 않는 경우 다음을 고려할 수 있습니다. \(0 \leq f_n \chi_E \leq f_{n+1} \chi_E \nearrow f \chi_E.\) 따라서 단조 수렴의 정리가 \(E\)에도 적용된다는 것은 분명합니다.

참조. 정리는 함수 순서 \(f_n\)가 증가하는 경우에만 적용됩니다. 감소의 경우 함수 \(f_n = \chi_{(n, \infty)}\)를 반례로 생각할 수 있습니다. 그런 다음 \(\chi_{(n, \infty)} \searrow 0\) if \(n \rightarrow\infty\) 입니다.

그러면 르베그 측정 \(m\) \(\infty = \int \chi_{(n, \infty)} \,d{m} \neq \int 0 \,d{m} = 0\)에 대해 단조 수렴의 정리가 성립하지 않는다는 것을 알 수 있습니다.

---

지난 번에 \(f \geq 0\)이 측정 가능하면 증가하는 측정 가능한 단순 함수 시퀀스 \(s_n\)가 있고 이 \(s_n\)에 대한 정수 값을 계산하여 \( \int_E s_n \, d{\mu } = \sum _{i=1}^{n2^n} \frac{i – 1}{2^n}\mu\left( \left\{x \in E : \frac {i- 1}{2^n} \leq f(x) \leq \frac{i}{2^n}\right\} \right) + n\mu(\{x \in E : f (x )\geq n\})\)도 보존되었습니다. 그러나 여기에서 \(f(x) = \displaystyle\lim_{n\rightarrow\infty} s_n(x)\)이므로 단조 수렴의 정리 \(\int_E f \,d{\mu } = \lim_{ n\rightarrow\infty} \int_E s_n \,d{\mu}\), 예상 결과를 제공합니다. 이는 지난 시간에 설명한 바와 같이 Lebeck의 적분은 절단 범위에 따라 면적을 계산하는 것으로 이해될 수 있음을 의미합니다.

다음은 단조 수렴 정리를 사용하여 유용한 결과를 쉽게 얻는 예입니다.

참조. 측정 가능 함수 \(f, g \geq 0\) 및 \(\alpha, \beta \in (0, \infty)\) \(\int_E \left( \alpha f + \beta g \right) \ ,d{\mu } = \alpha \int_E f \,d{\mu } + \beta \int_Eg\,d{\mu } .\)

입증하다. 측정 가능한 함수는 측정 가능한 단순 함수로 근사할 수 있으며 \(f, g \geq 0\)는 단조롭게 증가할 수 있습니다. 따라서 측정 가능한 단순 함수 \(f_n\), \(g_n\) \(0 \leq f_n \leq f_{n+1} \near f\), \(0 \leq g_n \leq g_{n+) . 1 } \narrow g\) 로 잡기.

그러면 \(\alpha f_n + \beta g_n \nearrow \alpha f + \beta g\) 및 \(\alpha f_n + \beta g_n\)은 단조롭게 증가하는 측정 가능한 단순 함수 시퀀스입니다. 단조 수렴의 정리에 따르면 \(\int_E \left( \alpha f_n + \beta g_n \right) \,d{\mu } = \alpha \int_E f_n \,d{\mu } + \beta \ int_E g_n \,d{\mu } \rightarrow \alpha \int_E f \,d{\mu } + \beta \int_Eg\,d{\mu }\).

물 공급에도 유사한 절차를 적용할 수 있습니다.

정리하다. 측정 가능한 함수 \(f_n:X\rightarrow(0,\infty)\) \(\sum_{n=1}^\infty f_n\)의 경우 측정 가능하며, 이는 단조 수렴의 정리가 말하는 것입니다. int_E \sum _{n=1}^\infty f_n \,d{\mu } = \sum_{n=1}^\infty \int_E f_n \,d{\mu }.\)

입증하다. \(\sum_{n=1}^\infty f_n\)은 측정 가능한 함수의 극한이므로 측정 가능합니다. 무한 급수를 부분합의 극한으로 생각하면 \(f_n \geq 0\) 부분합이 증가하는 것을 볼 수 있습니다. 따라서 단조수렴정리를 적용하여 결론을 얻는다.

---

단조 수렴 정리에 해당하는 또 다른 수렴 정리를 소개합니다. Fatou 기본형으로 알려져 있습니다.

정리하다. (Fatou) \(f_n \geq 0\)는 측정 가능하고 \(E\)는 측정 가능하다고 하자. 다음 사항이 적용됩니다. \(\int_E \liminf_{n\rightarrow\infty} f_n \,d{\mu } \leq \liminf_{n\rightarrow\infty} \int_E f_n \,d{\mu }.\)

입증하다. \(g_n = \displaystyle\inf_{k \geq n} f_k\)가 \(\displaystyle\lim_{n \rightarrow\infty} g_n = \liminf_{n\rightarrow\infty} f_n\)인 경우. \(g_n\)이 증가하고 \(g_n \geq 0\)이 증가하는 것을 쉽게 알 수 있습니다. \(g_n\)의 정의에서 모든 \(k\geq n\)에 대해 \(g_n\leq f_k\)이므로 \(\int_E g_n \,d{\mu }\leq\inf_{k\geq n } \int_E f_k \,d{\mu }\). \(n \rightarrow\infty\) = \(\int_E \liminf_{n\rightarrow\infty} f_n \,d{\mu } = \lim_{n \rightarrow\infty} \int_E g_n \,d{ \ 뮤} \leq \lim_{n \rightarrow\infty} \inf_{k \geq n}\int_E f_k \,d{\mu } = \liminf_{n \rightarrow\infty} \int_E f_n \,d{\ 뮤 }\) 여기서 첫 번째 등호는 단조 수렴의 정리에 의해 결정됩니다.

참조. 위의 증명은 단조 수렴 정리를 사용합니다. 반대로 이 정리를 가정하면 단조 수렴의 정리도 증명할 수 있다. 따라서 둘은 동일합니다. 증명은 생략합니다.

참조. 어쩐지 위와 비슷한 결론이 \(\limsup\)에도 적용되는 것 같다. 구체적으로 \(\int_E \limsup_{n \rightarrow\infty} f_n \,d{\mu} \geq \limsup_{n \rightarrow\infty} \int_E f_n \,d{\mu}\) . 불행히도 그것은 작동하지 않습니다. 반례로 앞에서 소개한 \(\chi_{(n, \infty)}\)를 다시 사용할 수 있습니다. 왼쪽은 0이지만 오른쪽은 \(\infty\)입니다. 나중에 소개하겠지만 위의 부등식은 \(\left| f_n \right| \leq g\)를 만족하는 함수 \(g\in \mathcal{L}^{1}\)가 있는 경우에만 적용됩니다.

참조. 우리는 Lebeck 적분의 몇 가지 속성을 소개하면서 마무리합니다.

1. 모든 합리적인 실수 \(M > 0\)에 대해 \(\left| f \right, \(f\)가 측정 가능하고 \(E\)에서 제한되고 \(\mu(E) < \infty\ ) | \leq M\), 즉 \(\int_E \left| f \right| \,d{\mu } \leq \int_E M \,d{\mu } = M\mu(E) < \infty\ ) 말할 수 있습니다. 따라서 \(f\in \mathcal{L}^{1}(E,\mu)\) . \(E\)의 척도가 유한하다고 가정하면 모든 유계 함수는 르베스크 적분 가능합니다.
2. \(f,g\in \mathcal{L}^{1}(E,\mu)\) 및 \(E\)에서 \(f\leq g\)까지 단조성이 성립함을 보여주기 위해 그렇게 합니다. 지금까지 단조성은 \(0 \leq f \leq g\)의 경우에만 증명되었지만 이를 확장하여 함수가 음수 값을 갖는 경우를 증명하고자 합니다. 따라서 플러스 부분과 마이너스 부분을 따로따로 생각하면 다음과 같이 쓸 수 있다. \(\chi_E (x) f^+(x) \leq \chi_E(x) g^+(x), \qquad \chi_E(x) g^-(x) \leq \chi_E (x) f^- (x)\) 이로부터 \(\int_E f^+ \,d{\mu } \leq \int_E g^+ \,d{\mu } < \infty, \qquad \int_E g^- \,d{ \ mu} \leq \int_E f^- \,d{\mu } < \infty\). 따라서 \(\int_E f\,d{\mu } \leq \int_E g \,d{\mu }\)가 유지되고 함수가 음수인 경우에도 단조성이 유지됩니다.
3. \(f\in \mathcal{L}^{1}(E,\mu)\) 및 \(c\in \mathbb{R}\)의 경우 \(cf\in \mathcal{L}^{1 ). }(E, \mu)\) . 왜냐하면 \(\int_E \left| c \right|\left| f \right| \,d{\mu } = \left| c \right| \int_E \left| f \right|\,d{\mu } < \infty\) . 적분도 가능하므로 실제 적분값의 계산에 있어서 선형성을 확립하는 것이 바람직하다. 지금까지 우리는 음수가 아닌 실수에 대해서만 증명했지만 이것을 확장하고자 합니다. \(c < 0\)인 경우에만 표시되어야 합니다. 이때부터 \((cf)^+ = -cf^-\) 및 \((cf)^- = -cf^+\) 다음이 성립합니다. \(\int_E cf \,d{\mu } = \int_E (cf)^+ - \int_E (cf)^- \,d{\mu } = -c \int_E f^- \,d{\mu } - (-c) \int_E f^+ \,d{\mu } = c\int_E f\,d{\mu }.\)
4. 측정 가능한 함수 \(f\)의 경우 \(E\)에서 \(a \leq f(x) \leq b\) 및 \(\mu(E) < \infty\)이면 \(\ int_E a \chi_E \,d{\mu } \leq \int_E f\chi_E \,d{\mu } \leq \int_E b \chi_E \,d{\mu } \는 \mu(E) \leq \를 의미합니다. int_E f \,d{\mu } \leq b \mu(E).\) \(f\)가 Lebesque 통합 가능하다는 사실은 \(f\)가 유계라는 사실을 사용합니다.
5. \(f\in \mathcal{L}^{1}(E,\mu)\) 및 측정 가능한 집합 \(A\subseteq E\)가 주어지면 \(f\)는 \(E\) 르벡의 일부입니다. 집합 \(A\)에 대해 적분도 가능합니다. 이것은 다음 부등식에서 볼 수 있습니다. \(\int_A \left| f \right| \,d{\mu } \leq \int_E \left| f \right|\,d{\mu } < \infty.\)
6. 측정값이 0인 세트에 대해 적분을 계산하면 어떻게 됩니까? \(\mu(E) = 0\)라고 하고 측정 가능한 함수 \(f\)를 적분합니다. 여기서 \(\min\{\left| f \right|, n\}\chi_E\)도 측정 가능하고 \(n \rightarrow\infty\) \(\min\{\left| f \right| , n\}\chi_E \narrow \left| f \right|\chi_E\) 마지막으로 단조 수렴 정리 \(\begin{aligned} \int_E \left| f \right| \,d{ \ 뮤} &= \lim_{n \rightarrow\infty} \int_E \min\{\left | f \right|, n\} \,d{\mu} \\ &\leq \lim_{n \rightarrow\ infty } \int_E n \,d{\mu} = \lim_{n \rightarrow\infty} 우리는 n\mu(E) = 0 \end{aligned}\) 을 얻습니다. 따라서 \(f \in \mathcal{L}^{1}(E, \mu)\) 및 \(\displaystyle\int_E f \,d{\mu} = 0\), 즉 적분은 다음과 같습니다. 0. 알 수 있습니다. 즉, 측정값이 0인 집합에 대해 적분하면 결과는 0입니다.^하나

다음 기사에서는 Lebeck의 수렴 정리를 소개합니다.

---

1. 단순화를 위해 \(0\cdot\infty = 0\)이 정의되었으므로 \(f \equiv \infty\)인 경우에도 적용됩니다.︎